Magnificent Hyperbolic Paraboloid

Those who met me on beBee know that I am always "pushing" the contents about interesting engineering stuff. I even created the Interesting Engineering, Technology and Discoveries hive, besides the already existing hives, to activate the beBee construction community to be more engaged in sharing and commenting. On this, not such an easy task, my fellow bee and 'dirt doctor’ @Ken Boddie has been of great help.
After my post about the geometry of the Platonic solids, which has been very well received on several social networks thanks to huge help in promoting it by dear @Milos Djukic, I decided to write about one of my favourite geometric forms, hyperbolic paraboloid, or shorten - hypar. The term 'hypar' was first introduced by the architect Heinrich Engel.
About Hypar
Shortly, a hyperbolic paraboloid is a doubly curved surface that resembles the shape of a saddle. It has a convex form along one axis and a concave form along the other. This unique design gives it a soaring shape.

In geometry, the hyperbolic paraboloid is a surface in three dimensions formed by translating (parallel displacement) a downward curving parabola along an upward curving parabola, producing a saddle surface. For this reason, the hypar counts as a translational surface.
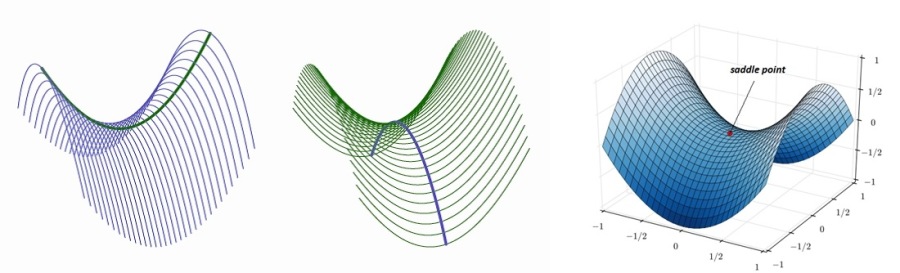
Its name – hyperbolic paraboloid, arises from the fact that the horizontal cross-sections are hyperbolas, while vertical cross-sections (parallel to the other two coordinate planes: xz and yz plane) are parabolas. The traces, as shown in the image below, are simply the intersections of a surface with planes parallel to the coordinate planes. When a hyperbolic paraboloid is sliced by horizontal planes we get hyperbolic traces (explained in a short video). The horizontal cross-sections are also called level curves.
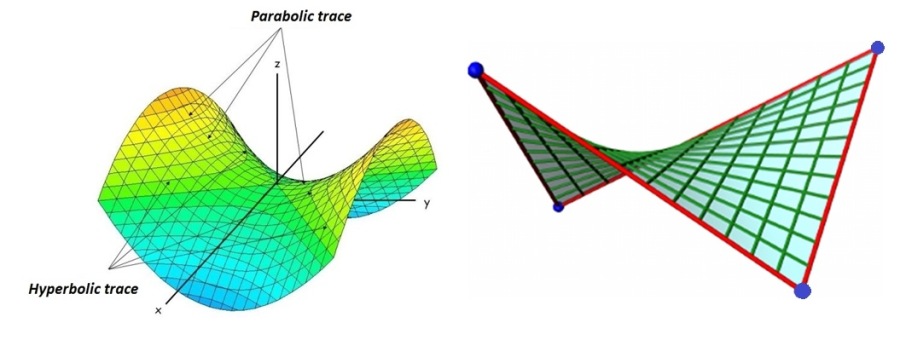
Hypar is both a translational and a ruled surface
Hypars can also be formed by two sets of straight lines called generatrices, or rulings. This means that despite being a curved surface, a hypar can be thus constructed with straight lines, just like in this video showing a hypar model made of skewers.

A surface that contains two sets of straight lines, or rulings, is called a doubly ruled surface. Through every one of its points (T) there are two distinct lines that lie on the surface, as shown in the image above.
An important reason for the use of hypars in construction is that they can be formed using straight lines. Consequently, the hyperbolic paraboloid is an ideal shell form, allowing the use of straight boards for formwork.
Particularly is interested how hypars can be joined together, at their edges, to make beautiful structures.
Strength Through Curvature - Hypar Thin Shell Concrete Roofs
Fernand Aimond (1902-1984) can be considered as the father of the thin hypar concrete shells, who also formulated the membrane theory of the hypar. He designed and constructed several hypar roofs in France in the 1930s for aircraft hangars and workshops.
But a master of hypars and joining hypars was Spanish architect, engineer, structural artist and builder Felix Candela (1910-1997), who popularized the use of hypars for reinforced concrete construction. Candela was influenced by Aimond and gave credit to his work. He also followed the fundamentals of Eduardo Torroja's work, a famous Spanish structural engineer renowned for his development of reinforced concrete and thin concrete shell structures. Candela identified himself more as an engineer and builder and studied structural engineering on his own.
I must say.... that although an architect by training, in practice I am a constructor and building contractor.
Candela, 1955
He designed and built many innovative thin-shell concrete roof structures. Most of these structures were built in Mexico in the 1950s and 60s. That was the “golden era” for thin shell construction. Candela constructed over 300 shells during these decades. He was the greatest practitioner of shell design whose name has become synonymous with the hyperbolic paraboloid.
His thin concrete vaulted shells were made of reinforced concrete mixed and poured in situ, over wooden formwork. The thin shell roofs allowed the minimum thickness of concrete while having great strength and stiffness at the same time.
The strength comes from form, not mass. Hypar roofs gain their strength from double curvature that allows hypar structures a great resistance to bending. The doubly-curved shape strikes a balance between tension and compression forces, allowing hypar structure to remain thin, yet surprisingly strong.
**********
Candela constructed his first hypar shell for the University of Mexico in 1951. The Cosmic Rays Laboratory main structure is a shell made of two adjacent hypar saddles (12 meters in total length and 11 meters wide) supported by a platform and stiffened by three arches. It is one of the thinnest cast-in-place (in situ) concrete structures ever built. At its thickest point, the concrete reaches only 15 mm that the cosmic radiation could be measured through it. The shell remains in a good condition for more than 60 years.

The second image clearly shows the straight-line form boards following the ruling lines (double ruling) of the geometric form. This early hypar structure was an overture to Candela's outstanding career as a shell builder.
**********
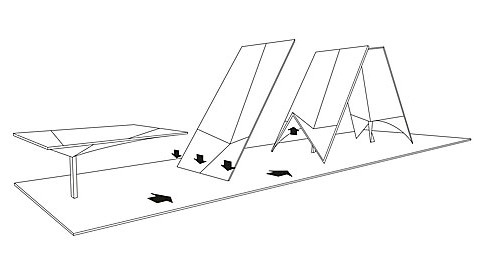
In 1952 Candela started experimenting with the umbrella structures of four identical quadrants, called tympans. The shell geometry was created by joining four straight-edged hypars whose sides rose upwards away from the central column (as if an umbrella blown upward). Umbrella structure is a type of inverted pendulum. Precisely, it is a cantilevered structure. The basic structural scheme of an umbrella consists of a foundation, only one column (with an embedded pipe to catch the rainwater) and a roof.
Inspired by Aimond’s sketches, Candela created the solution of umbrella shell, without the edge beams. Candela's concept also included the ingenious design of an inverted umbrella structure as footings to distribute the weight of the structure onto the poor quality Mexican subsoil. The footing was simply an inverted form of the umbrella shell.
Below is the famous photo of his second experimental umbrella in 1953, in which he tried to find the optimum rise and area of an umbrella. It shows load testing with twenty-five workers who climbed the shell.

Below is shown an umbrella structure under construction, with scaffolding and formwork, and carefully placed reinforcement.

Candela experimented with umbrella forms during the 1950s. The umbrellas became asymmetrical and with various inclinations. Over the years, his common umbrella form progressed to the folded hypar. By placing several umbrellas, side by side, Candela designed large roof surfaces, mostly for low-cost industrial construction. These structures were built in a very short time and with reusable formwork.
Later, he developed a new form of the rectangular umbrella by arranging folded hypars. The first such umbrella structure was constructed for the Candelaria Subway Station in Mexico City, built in 1968.
Based on this form, he also created some interesting structures that appeared to defy gravity, such as the bandshell in Santa Fe, Mexico City, completed in 1956.

The ground-breaking design of the hypar umbrella was inspired by natural trees complemented by Candela's imagination and the implementation of technical innovations.
**********
The folded hypars, an adaptation of the common umbrella design, Candela used to create dramatic roofs of large spaces, such as the roof for the Church of the Miraculous Medal (Milagrosa), built in 1955 in Mexico.
The church is a remarkable building. It is somewhat reminiscent of Gaudi's forms. The structure is a combination of super-warped hypar surfaces with a thickness of 4 cm or less. Even the bell tower is made of hypars. It seems as if Candela wanted to see how much can be done with this type of structure.
As clearly explained in the image below, the form for the roof structure consists of the hypars derived from asymmetrical umbrella forms that were tilted and then pleated to create triangular openings.
The roof shells and interior columns merge together in extraordinary geometry. Candela shows in Milagrosa his virtuous performance in the use of hyperbolic paraboloids.

More about this design on the following video
The Milagrosa is also one of the early examples of the brutalist-style building with the sculptural exposed concrete.

Outside and inside view of this amazing roof with visible imprints of the form boards
Here Candela used a similar construction procedure as on his previous structures, including the use of inverted umbrella form for the foundations. The formwork for Milagrosa differed from that of his other shells because the warping is too large. To provide adequate curvature, Candela used wedge-shaped thick boards.

The casting of the roof with no mechanical equipment - concrete was placed manually using buckets
**********
One of his major works is the Lomas de Cuernavaca Chapel (“hills of Cuernavaca”), Mexico, built in 1958. Candela used a single hypar surface to get an open-air chapel with a structural form of pure aesthetics. The Cuernavaca Chapel shell is self-supporting with a span of 30 m and dramatic curvature. The open end of the chapel rises to a height of 24 meters and has visible thinness of 4 cm that represents the frontiers of the form.

As seen in the image below, the straight timber members (framework) were used to develop curve form, because a double-curved hypar can be generated by straight lines. The form boards were then laid on the top in the other direction. Imprints of these form boards are visible on the inner side of the concrete shell.

(1) The formwork clearly shows the hyperbolic paraboloid is a ruled surface, (2) Scaffoldings for the concrete shell

(1)The concrete shell immediately after the removal of the scaffolding, (2)Visible imprints of the form boards
**********
In 1958, Candela completed his most significant work, the Los Manantiales Restaurant in Xochimilco, Mexico City.
The Xochimilco shell is composed of four intersecting hypars with free curved edges. The soaring shape at the edges resulted in a simple and gracefully thin-shell structure.
Most shells prior to Candela have edge ribs to prevent crack from the edges inward. Candela found the free-edge innovative solution which was elegant and efficient at the same time. His solution has focused on the groins rather that the edges. Each of Los Manantiales’ eight groins is thickened into a V-shaped beam. These beams enhance the groins’ stiffness, reducing bending and deflection, and thereby eliminating normal edge forces. At the supports, the V-beams anchor into umbrella footings.
Journal of IASS: Burger and Billington
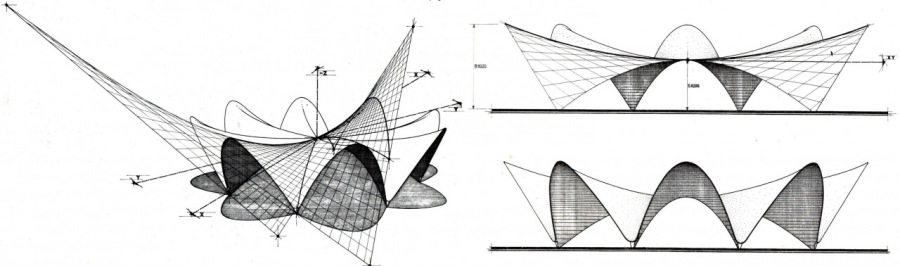
In these original drawings, Candela clearly shows the form of the Manantiales Restaurant shell. It is an eight-sided groin vault composed of four hyperbolic paraboloid saddles that intersect at the centre point. The form was original and unexplored at that time. The innovative use of V-shaped beams allows edges free of stiffening beams and produced a radical shell thickness of only 4 cm.

The plan is radially symmetric with a maximum diameter of ca. 42 meters. Groins spanning around 32 meters between supports. At the centre the shell has a height of 5.8 m and the edges rise to 9.9 m.

Narrow boards, used as formwork, followed the straight-line rulings that form the hypar surface. A layer of cement grout, laid under concrete, created a smooth inner surface. The concrete was placed by hand, one bucket at a time.
The V-shaped beams were reinforced with steel, while the shell has only nominal reinforcement to address temperature effects that can cause cracking.
The almost 60-year-old shell is still structurally intact and generally in fine condition. It represents a testimony of Candela as a structural artist of great merit.
**********
The underwater restaurant at L'Oceanogràfic, a large oceanographic park in Spain, and the access building to the same park were the Candela's final projects. These shells were designed by Candela shortly before his death in 1997, becoming his posthumous works.
For the restaurant design, Candela re-elaborated the shell structure built in 1958 in Xochimilco (Mexico) composed of eight radially symmetrical lobes, each lobe as part of a hypar. The shell is only 6 cm thick that gradually increases up to 22.5 cm at the intersection of the ribs.
The geometry of the concrete shell structure for the entrance building was based on the hand-drawn sketches by Candela. This shell consists of the intersection of three hyperbolic paraboloids.
The geometry of the restaurant and entrance building

The underwater restaurant and the entrance building
The oceanographic park is integrated into the complex known as the City of Arts and Sciences, a cultural and architectural complex designed by Spanish architect Santiago Calatrava in partnership with Candela. The park was opened in 2003, while the whole complex was finished in 2010.
The shells are made of steel fibre reinforced concrete (SFRC) with reinforcement netting on the mid-surface of the shell. The concrete was applied with a shotcrete process onto wooden formwork that was supported by shoring towers. The process also included superficial finishing. The use of SFRC improved the shell’s tensile stress capabilities.

(1) (2) Restaurant’s roof under construction – 3D space framework up to a height of 13.70 m, (3) The shotcrete process on the entrance building roof

Concrete shells immediately after the removal of framework

Both buildings were designed to open out from the ponds like water lilies
Candela’s work continues to inspire contemporary designers such as Santiago Calatrava, another great Spanish architect who is also PhD in civil engineering (structural engineer). Candela, who was teacher of Calatrava, highly influenced the Calatrava’s works.
Geometry Meets Music
The Philips Pavilion was a temporary structure designed for Expo '58 in Brussels. The design was done by Le Corbusier in collaboration with the Greek composer Iannis Xenakis, an architect and engineer, who carried out most of the designing.
The goal was to build the pavilion to demonstrate the sound and light possibilities of Philips' technologies in those days. The structure supposed to be self-supporting and column-free, a hollow structure with acoustic qualities. Xenakis found a solution for the shape of the building in a series of conjoined curved planes forming a tent-like enclosure.
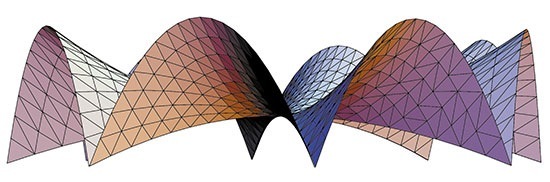
The chosen design was a cluster of nine hyperbolic paraboloids with a stomach-shaped floor plan (shown on the model below). Over 500 spectators might have been accommodated inside the pavilion for an eight-minute spectacle of light and sound called Poème électronique, by composer Edgard Varèse. People were sitting and lying in the darkroom and watched visual effects along the walls of the pavilion.

The following video is a short presentation of the used design and its geometry.

The final structure was 22 meters high and certainly pushed the limits of engineering of that time.

Coloured photographs of the Philips Pavilion at the Brussels World's Fair in 1958
To build such a complex form Xenakis proposed a structural system of prefabricated concrete panels hung in tension on the 7 mm wire cables, which were laid on both side of the shell. This ingenious solution also included about 2000 precast panels 5 cm thick panels, built in a hangar shed from simple sand moulds that matched the curvature of the pavilion. The size of the precast slabs was about 1 square meter with a light reinforcement mesh to prevent breakage during transportation to the site.

Moulded sand hill for casting panels
The steel cables were positioned inside and outside of the shell, following the ruling lines of hypar geometry, and anchored to the concrete ribs and foundation beam that formed the base of the pavilion. The "Strabed " system used for mounting prestressing cables. After erecting the panels, the entire structure was post-tensioned. Once the panels were erected, the entire structure had been post-tensioned, making a monolithic structure. The outside of the shells including the prestressing wires were covered with aluminium paint and the interior plastered with a sound-absorbent layer of asbestos felting.

(1) The precast slabs had been placed in the position and filled with mortar, (2) After erecting the panels, the prestressing wires were tensioned with a special jack
At the edges of each hyperbolic paraboloid shell (lines of intersection) were cylindrical concrete ribs, 40 cm in diameter, as the structural elements cast in situ. The scaffolding wooden beams followed the ruling lines of the hyperbolic paraboloid shells.
The second image below shows the numerous prestressing wires of high-tensile steel, which were applied on both surfaces of the shell and left visible.

The original pavilion was demolished in 1959. In recent years, there have been attempts to rebuild the pavilion in the hometown of the Philips Company, Eindhoven, Holland.
This work of art represented a phenomenon through its synthesis of architecture, visual media and music, and left its mark on history.
**********
In this post, I presented only a part of many astonishing structures based on the geometry of the hyperbolic paraboloid. Besides the form and shape of these structures, I also tried to present the construction process which is quite remarkable. The used methods of construction were both material and labour intensive. At that time, almost 60 years ago, those methods were the only possible.
The thin concrete shells are not as popular as they once were, in the golden era of concrete shell structures prior to 1968. Recent advances in concrete technology should affect the cost of construction and may help revive the interest in this structural form, particularly in the magnificent hyperbolic paraboloid form.
Sources:
1. Journal of IASS, an article by Noah Burger and David P. Billington
2. Journal of the International Association for Shell and Spatial Structures · March 2010
3. Construction of JChypar, a thin fibre reinforced concrete shell structure
4. Construction of the pavilion in prestressed concrete, by H.C.Duyster
5. Philips Pavilion EXPO 1958 Bruxelles, by Fausto Giovannardi
6. The Princeton University Art Museum
7. Superficies Arquitectónicas Singulares · Julio 2011
u Civil Engineering i u Još 1 grupa
Članci od Lada 🏡 Prkic
Pogledaj blog
I am a civil engineer and love everything about engineering and architecture. I love watching shows ...

I have a life motto that I put on my beBee profile page: The more I learn, the more I realise there' ...

From my first step into the world of social media, I was fascinated by people who regularly inhabit ...
Vezani profesionalci
Možda će vas zanimati ovi poslovi
-

sap technical consultant
Pronađeno u: beBee S2 HR - prije 4 dana
Atos Zagreb, HrvatskaEviden an Atos business in Croatia is a certified "Great Place to Work" employer. The opinion of employees plays a decisive role in selecting the winners of this global award given to the best employers. We are the first and only company in Croatia that won GPTW four years in a r ...
-

Agent/ica u odjelu teleprodaje
Pronađeno u: beBee S2 HR - prije 1 dan
Transcom Croatia Osijek, Hrvatska Puno radno vrijemeOvo je posao za sve koji su spremni učiti i rasti, a mi smo tu da pružimo početnu obuku i kontinuiranu podršku na tom putu. Bez obzira jesi li tek na početku karijere ili tražiš novi izazov, kod nas ćeš naći priliku za ostvarenje svojih profesionalnih ciljeva te pritom biti nagra ...
-

Finance Operations Senior Specialist
Pronađeno u: beBee S2 HR - prije 4 dana
Teva Pharmaceuticals Zagreb, HrvatskaWho we are · Together, we're on a mission to make good health more affordable and accessible, to help millions around the world enjoy healthier lives. It's a mission that bonds our people across nearly 60 countries and a rich, diverse variety of nationalities and backgrounds. Wor ...

Komentari
Lada 🏡 Prkic
prije 1 godinu #49
Hypar found its way because it is ideal for making concrete shells. Since it is a doubly ruled surface, it can be covered with two families of straight lines, which helps formwork construction. Thanks for stopping by, Zacharias.
Lada 🏡 Prkic
prije 1 godinu #48
It's never too late to read old posts. Thanks for giving my article a new life by reading and commenting, Neil. 🤗
Lada 🏡 Prkic
prije 1 godinu #47
Thank you, @Javier 🐝 CR 🇺🇦🇪🇸, for solving the problem with editing. I fixed some broken links. Thanks for sharing. 🤗
Zacharias 🐝 Voulgaris
prije 1 godinu #46
Intriguing. The whole thing reminds me a bit of Bucky Fuller's geodesic dome, though not nearly as sophisticated. Still, a profound shape nevertheless. Cool how it found its way to architecture too. Cheers
Neil Smith
prije 1 godinu #45
Every day is a schoolday and so this is my lesson for today.
I appear to have missed it first time around so good to catch up belatedly.
Javier Cámara-Rica 🐝🇪🇸
prije 2 godine #44
LinkedIn sees external articles like potential competitors 😍😍. It is back thanks to @Leticia Gómez López . @Ken Boddie please feel free to contact her if you see anything else you miss!
Lada 🏡 Prkic
prije 3 godine #43
Thanks again Debesh. It is "cross-pollination" between LinkedIn and beBee in action. :) As I see it, the LinkedIn algorithm doesn't like beBee's articles and reduces their visibility.
Debesh Choudhury
prije 3 godine #42
Lada 🏡 Prkic
prije 5 godina #41
Thank you, Ken. It was a phase of writing "encyclopedic" articles. :) You made me laugh, as always. The title pic indeed looks like nuns' starched headwears. :)
Ken Boddie
prije 5 godina #40
Lada 🏡 Prkic
prije 5 godina #39
Randall Burns
prije 6 godina #38
LOL! :-)
Lada 🏡 Prkic
prije 6 godina #37
My Professional Liability insurance, as a certified (chartered) engineer, is provided by Croatian Chamber of Civil Engineers. The insured sum can go up to about 500,000 USD and shall not be less than about 200,000 USD.
Lada 🏡 Prkic
prije 6 godina #36
My Professional Liability insurance, as a certified (chartered) engineer, is provided by Croatian Chamber of Civil Engineers. The insured sum goes up to about 500,000 USD.
Lada 🏡 Prkic
prije 6 godina #35
Thanks, Randall. I wrote about concrete shells and you about mussel shells. :-)
Lada 🏡 Prkic
prije 6 godina #34
Yes, they are many timeless and beautiful structures, Melody. You named two more beauties that also deserve to be mentioned in my next post about the striking use of parabolas and spherical geometry in construction. Congrats on being on the Sydney Opera House stage.
Randall Burns
prije 6 godina #33
Melody Green
prije 6 godina #32
Lada 🏡 Prkic
prije 6 godina #31
Thanks for stirring the pot, Franci. :)
Lada 🏡 Prkic
prije 6 godina #30
It's the combination of creative mind and geometry that produced such amazing structures, just like Candela who was both an architect but also a structural engineer and builder.
Lada 🏡 Prkic
prije 6 godina #29
Thank you, dear An\u0111ela Bogdan. This topic is one of my favourites - merging geometry and thin concrete shells. Another post about the use of parabolas in construction is in the draft for a long time. Such posts are very demanding, as you already know, and can't be written in a couple of hours like the most posts on social media. Thanks for encouraging to publish it in Građevinar. We can talk about it. :)
Lada 🏡 Prkic
prije 6 godina #28
Lada 🏡 Prkic
prije 6 godina #27
My apologies for the belated response, Jerry. I love this shape and its simplicity in complexity. I'm in awe with engineers ingenuity in making such complex and remarkable structures, like Candela's Milagrosa, by joining different forms derived from the same basic shape. Not to mention the Philips Pavilion and its ingenious structural solution behind the design.
Debasish Majumder
prije 6 godina #26
Jerry Fletcher
prije 6 godina #25
Lada 🏡 Prkic
prije 7 godina #24
Thank you for stopping by Phil. When it comes to Candela’s shells, everything began with the new and original form of structure unexplored at that time. He experimented with the form and tried to find how much can be done with such kind of structure. In this case, I could say that form follows the structure up to a maximum limitation of its geometric form. Hope it sounds meaningful. :-) Thanks for the interesting question.
Lada 🏡 Prkic
prije 7 godina #23
Thank you for stopping by Phil. When it comes to Candela’s shells, everything began with the new and original form of structure unexplored at that time. He experimented with the form and try to find how much can be done with such kind of structure. In this case, I could say that form follows the structure up to a maximum limitation of its geometric form. Hope it sounds meaningful. :-) Thanks for the interesting question.
Lada 🏡 Prkic
prije 7 godina #22
Thanks for stopping by Phil. When it comes to Candela’s shells, everything began with the new and original form of structure unexplored at that time. He experimented with the form and try to find how much can be done with such kind of structure. In this case, I could say that form followed the structure up to a maximum limitation of its geometric form.
Lada 🏡 Prkic
prije 7 godina #21
Another beautiful example of a hyperbolic structure with amazing stained glass windows. Not a hypar, but it's magnificent. Thank you Dilma. Keep it sharing!
Lada 🏡 Prkic
prije 7 godina #20
Thank you my friend for cross pollination on both platforms. 🐝 I chose the building icon because I am a builder. :-)
Lada 🏡 Prkic
prije 7 godina #19
I am glad you like it, Claire. Hadid and Calatrava both used many elements of hyperbolic geometry in their works. Thank you for stopping by and commenting. Thanks for sharing, too.
Lada 🏡 Prkic
prije 7 godina #18
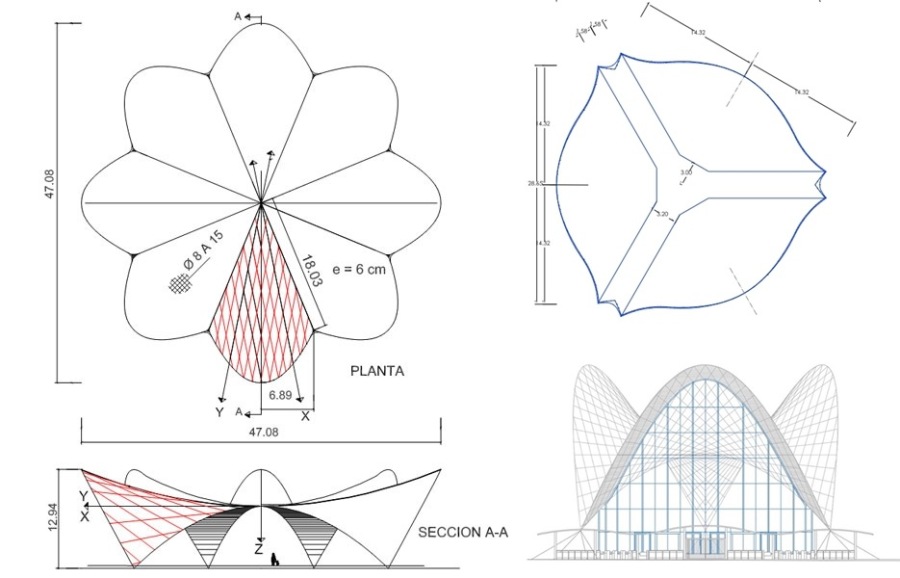
Dear \ud83d\udc1d Fatima Williams, you noted one of the most beautiful buildings in the world. Its complex shell form of the 'lotus petals' consists of many geometric shapes and forms. I can only imagine how exciting it must have been to see this magnificent building. Thank you for commenting and sharing this video. Enjoy exploring! :-)
Phil Friedman
prije 7 godina #17
🐝 Fatima G. Williams
prije 7 godina #16
🐝 Fatima G. Williams
prije 7 godina #15
Lada 🏡 Prkic
prije 7 godina #14
Much obliged, dear Prof. Milos Djukic. :-)
Lada 🏡 Prkic
prije 7 godina #13
Thanks again. I would also like to know his response.
Milos Djukic
prije 7 godina #12
Lada 🏡 Prkic
prije 7 godina #11
Ken, you’re right about the length of the post, but I decided to include at least the most significant thin concrete hypar shells. Perhaps a chapter about Philips Pavilion could be a separate post. But I hope that a person who is interested in this topic will read the entire post. I think that only Gerald Hecht wrote the longer post than I. ✍️ 👨🔬 https://www.bebee.com/producer/@gerald-hecht/on-the-behavioral-part-of-behavioral-pharmacology Such versatile professional you described in the comment is a master "ingmarch". I can't find the better acronym. :)
Ken Boddie
prije 7 godina #10
Lada 🏡 Prkic
prije 7 godina #9
Thanks for commenting Mohammed. I just wanted to present this beautiful geometric form and its possibilities of the sculptural use in architecture and construction, focusing on reinforced concrete as a material for hypar shells. The richness of this form is most evident when hypars are connected edge-to-edge, resulting in variety of beautiful thin curved surfaces. Zaha Hadid used many elements of hyperbolic geometry in her works and designed shells of complex shapes and forms.
Lada 🏡 Prkic
prije 7 godina #8
Lada 🏡 Prkic
prije 7 godina #7
Lada 🏡 Prkic
prije 7 godina #6
Thanks for the offer Julio. Glad to know that ambassadors also provide tour guide services. :))
Julio Angel 🐝Lopez Lopez
prije 7 godina #5
Julio Angel 🐝Lopez Lopez
prije 7 godina #4
Pues cuando vengas no necesitas guia, yo te enseño la ciudad. Servicio gratuito de embajador beBee :-)
Lada 🏡 Prkic
prije 7 godina #3
Thank you Julio Angel Lopez Lopez. The Oceanographic was an inspiration for this post about hypar shells. Barcelona and Valencia are on my wish list.
Julio Angel 🐝Lopez Lopez
prije 7 godina #2
Lada 🏡 Prkic
prije 7 godina #1