Geometry, All Around Us

Geometry is all around us, and we are surrounded by myriads of geometric forms, shapes, and patterns. Every living organism and all non-living things have an element of geometry within. Understanding the natural world requires an understanding of geometry.

Where there is a matter, there is geometry. (Johannes Kepler)

For me, geometry is a fascinating subject. As the subject of learning, geometry requires the use of deductive reasoning, a logical process in which a conclusion is based on the multiple premises that are generally assumed to be true (facts, definitions, rules). Learning geometry also develops visualization skills and spatial sense - an intuitive feel for form in space.

Geometry is essential in architecture and engineering fields and mostly used in civil engineering. Thorough knowledge of descriptive geometry is definitely required for civil engineers and helps engineers to design and construct buildings, bridges, tunnels, dams, or highways. It has been, by the way, one of my favourite subjects during my university years.

I use mathematics and geometry almost my whole life. To write about geometry in a way that does not look like a boring lecture is challenging. It is, therefore, my intention to write this post in a manner of a picture book – geometry in words and pictures, because I prefer visualization wherever possible. I shall try to skip formulas, theorems, rules. There will be only a little math.

This piece is a review of some interesting geometric forms, which are particularly impressive to me. 

PERFECT FORMS

Necessary Introduction

Polygons (many sides in Greek) are closed plane figures with straight sides. Regular polygons are polygons whose all sides are equal in length. A regular polyhedron (pl. polyhedra) is a three-dimensional solid whose all faces are regular polygons.

Platonic Solids

These regular polyhedra are called the Platonic solids or perfect solids, named after the Greek philosopher Plato although he is not the first who described all of these forms. 

The Platonic solids are symmetrical geometric structures, bounded by regular polygons all of the same size and shape. Moreover, all edges of each polygon are the same length and all angles are equal. The same number of faces meets at every vertex (corner or point).

Furthermore, if you draw a straight line between any two points (vertices) in any Platonic solid, this piece of the straight line will be completely contained within the solid, which is the property of a convex polyhedron.

An amazing fact is that can be only five different regular convex polyhedra. These perfect forms are:

1. Tetrahedron
2. Octahedron
3. Hexahedron (cube)
4. Icosahedron
5. Dodecahedron

Plato was deeply impressed by these forms and in one of his dialogues Timaeus, he expounded a "theory of everything" based explicitly on these five solids. Plato concluded that they must be the fundamental building blocks—the atoms—of nature and he made a connection between five polyhedra and four essential (classical) elements of the universe; tetrahedron → fire, cube → earth, octahedron → air, icosahedron → water, and the dodecahedron with its twelve pentagons was associated with the heavens and the twelve constellations.

Later, Aristotle, who had been Plato's student, introduced a new element to the system of the four classical elements. He classified aether as the “fifth element” (the quintessence). He postulated that the stars (cosmos itself) must be made of the heavenly substance, thus aether. Consequently, ether was assigned to the remaining solid --dodecahedron.

Why Only Five?

Geometric argument and deductive reasoning

Postulates:

1.  At least three faces must meet at each vertex to form a polyhedron.
2. The sum of internal angles of polygons that meet at each vertex must be less than 360 degrees (at 360° they form the plane, i.e. the shape flattens out).

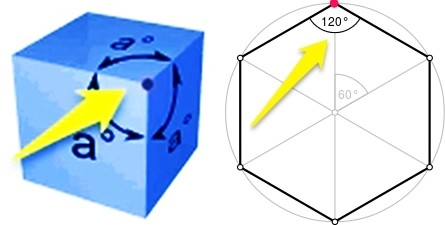
If solid's faces that meet at each vertex are regular triangles, squares, and pentagons, the sum of angles at each corner is less than 360°. Forming a regular solid of hexagons won’t work because hexagon has internal angles of 120°, and in the case where a minimum of 3 hexagonal faces meet at one vertex it gives → 3×120°=360°, thus the shape flattens out.

Consequently, there is no platonic solid formed from hexagons or any regular polygon of more than 5 sides.

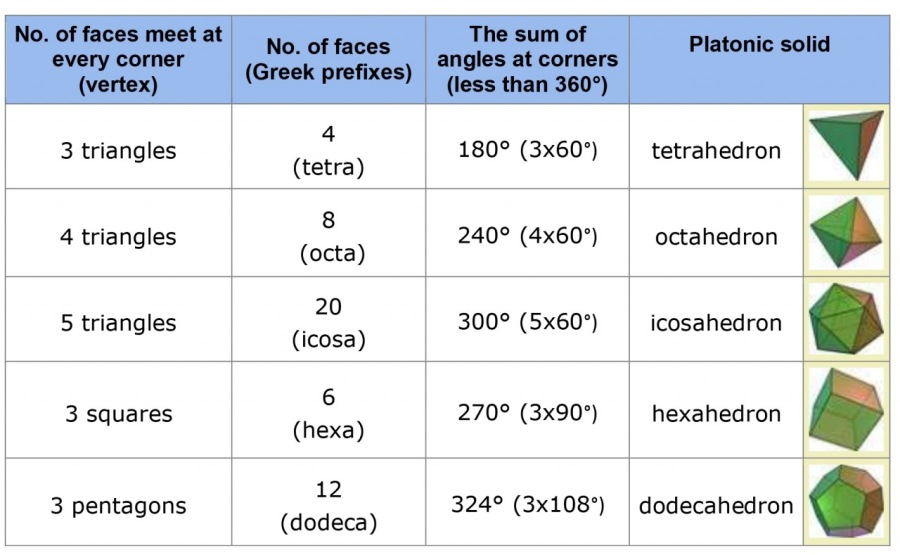
The table below is a result based on previous arguments and reasoning. Solids are made only of regular triangles, squares, and pentagons. There are only five possibilities, thus five regular solids. Any other combination is not possible!

The mathematical proof given by Euler's formula confirmed that there are exactly five Platonic solids.

THE BEAUTY OF PLATONIC SOLIDS' GEOMETRY

Spheres and Platonic Solids

Each solid will fit perfectly inside of a sphere → circumsphere and all the angular points (vertices) are touching the edges of the sphere with no overlaps. Nonetheless, the inscribed sphere → insphere touches all the faces.

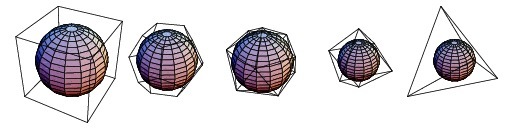
Nested Platonic Solids

Platonic solids have the ability to nest one within the other. The corners of the inner Platonic solid touch the vertices or the edges of the outer solid. The amazing animation below shows the configuration of all five Platonic solids, each fits perfectly inside the other.

The video shows how (transparent) dodecahedron opens to reveal a cube inside, which opens to allow a tetrahedron to come out, then octahedron, which opens to reveal the inner icosahedron. All the Platonic solids are harmoniously nested one inside the other.

Duals of Platonic Solids

Each Platonic solid has a dual Platonic solid. If a midpoint (centre) of each face in the platonic solid is joined to the midpoint of each adjacent face, another platonic solid is created within the first.

It occurs in pairs between the solids when the number of faces in one solid = the number of vertices in another.

• The tetrahedron is self-dual (its dual is another tetrahedron), the only one with 4 faces and 4 points
• The cube and the octahedron form a dual pair (an octahedron can be formed from the cube, and vice versa), 8 faces in cube=8 points in the octahedron, or 6 points in cube = 6 faces in an octahedron
• The dodecahedron and the icosahedron form a dual pair (a dodecahedron can be formed from an icosahedron, and vice versa), 12 faces in dodecahedron = 12 points in an icosahedron, or 20 points in dodecahedron=20 faces in an icosahedron

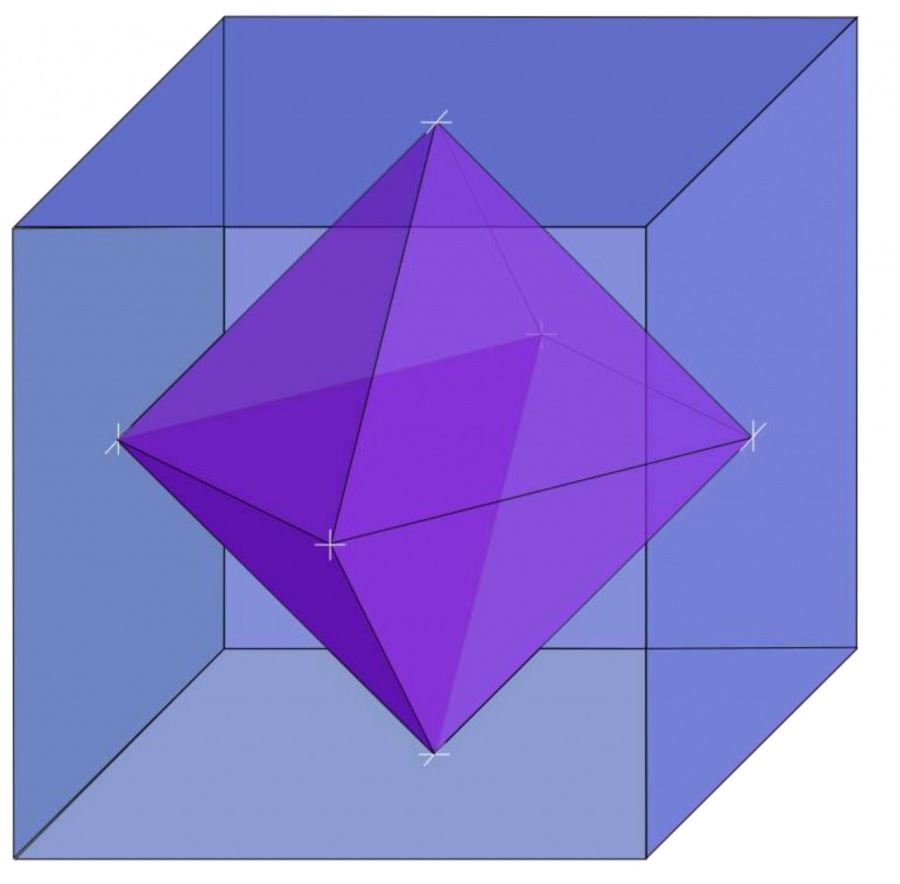
The image above clearly shows how the octahedron occurs from the cube - putting a vertex at the midpoint of each face gives the vertices of dual polyhedron – octahedron. In vice versa, by connecting all midpoints of an octahedron’s faces occurs a cube, like in the image below.

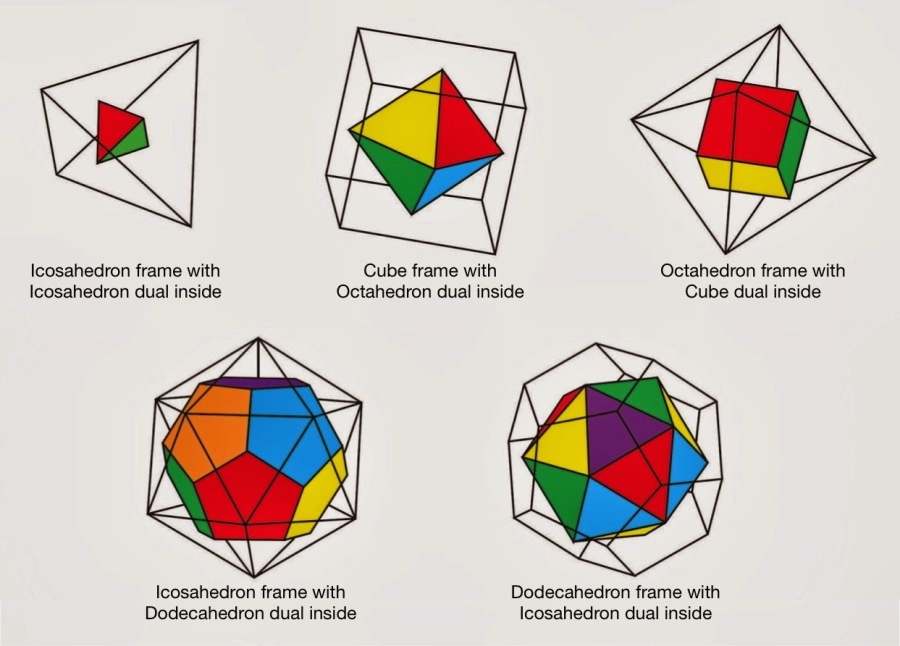
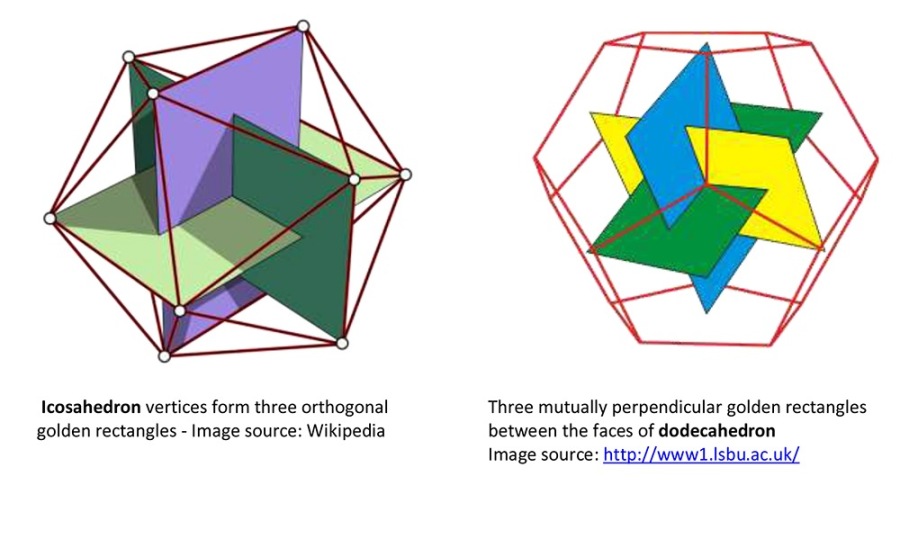
The Golden Ratio in Icosahedron and Dodecahedron

The icosahedron and his dual pair the dodecahedron are uniquely connected with the golden ratio by virtue of three mutually perpendicular golden rectangles which fit into both. These mutually bisecting golden rectangles can be drawn connecting their vertices and mid-points respectively.

A golden rectangle is a rectangle which side lengths are in the golden ratio, 1: φ (the Greek letter Phi), where φ is approximately 1.618.

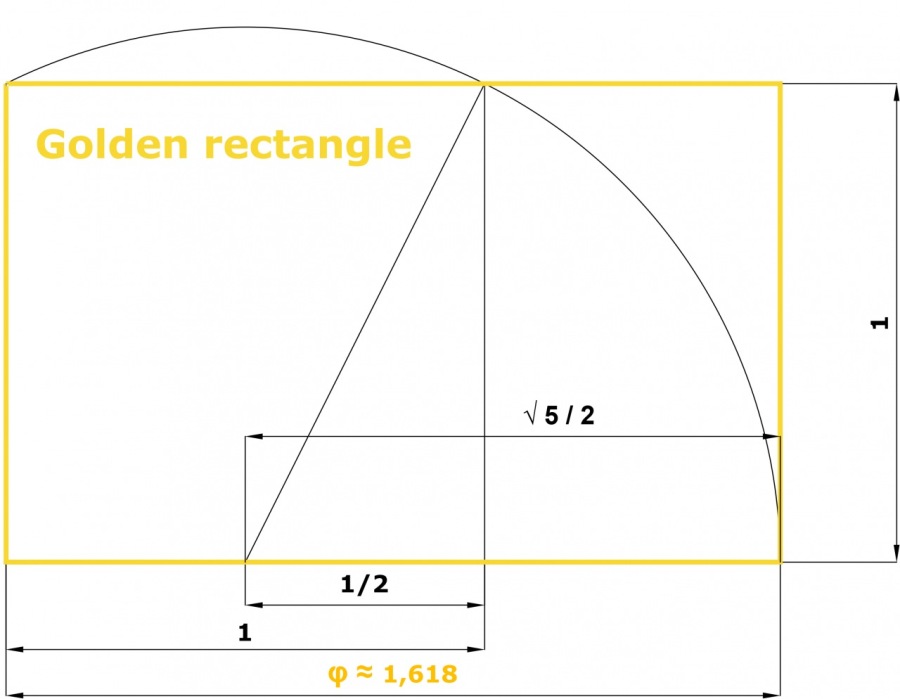
Since the ancient days, geometricians have known that there is a special, aesthetically pleasing, rectangle with width 1, length x, and the following property: dividing the original rectangle into a square and new rectangle, as illustrated in the image above, arises a new rectangle which also has sides in the ratio of the original rectangle.

This curious mathematical relationship, widely known as the golden ratio, was first recorded and defined in written form around 300 BC by Euclid, often referred to as the father of geometry, in his major work Elements. 

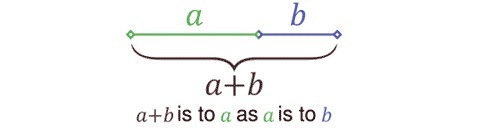
The golden ratio refers to a specific ratio between two numbers which is the same as the ratio of the sum of those numbers to the larger of the two original quantities. The value of the golden ratio is an irrational number, which is 1.6180339887......  (assuming that a is greater than b, and b is greater than zero).

Fractal Structure of Platonic Solids

Each Platonic solid has its own fractal structure, the same repetitive patterns that fit within each other. The two famous Platonic fractals are the Menger Sponge for the cube and the Sierpinski tetrahedron for the tetrahedron, a three-dimensional analogue of the Sierpinski triangle, also called the Sierpinski sponge or tetrix.

The illustrations show Menger sponge after the fourth iteration of the construction process, and a Sierpinski square-based pyramid (tetrahedron) and its 'inverse' after the third iteration. On every face, there is a Sierpinski triangle and infinitely many contained within. 

Of all other Platonic fractals, particularly interesting is the Sierpinski dodecahedron. The image below shows a dodecahedral-cornered supercluster, in which a smaller dodecahedron is placed in each corner of the original solid to get a dodecahedral cluster. The process can be repeated indefinitely.

PLATONIC SOLIDS IN NATURE

These regular structures are commonly found in nature, but they are generally hidden from our perception. The first manifestation of Platonic solids in nature is in the shape of viruses. Many viruses have a viral capsid, a protein shell that protects and encloses the viral genome, in the shape of an icosahedron. A regular icosahedron is an optimum way of forming a closed shell from identical subunits.

Of all Platonic solids only the tetrahedron, cube, and octahedron occur naturally in crystal structures. The regular icosahedron and dodecahedron are not amongst the crystal habit. 

Iron pyrite, known as fool's gold, often form cubic crystals and frequently octahedral forms. Calcium fluoride also crystallizes in cubic habit, although octahedral and more complex forms are not uncommon. 

Tetrahedrite gets its name for its common crystal form - tetrahedron. Sphalerite also occurs in a tetrahedral form.

All Platonic solids occur in a tiny organism known as Radiolaria, which are protozoa – single-celled organisms widely distributed throughout the oceans whose mineral skeletons are shaped like various regular solids.

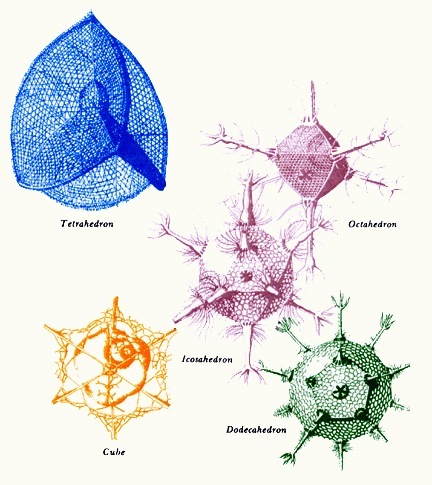
These Platonic forms also emerge in the mitosis of a developing zygote, the first cell of the human body.  The first four cells occur by dividing, form a tetrahedron.

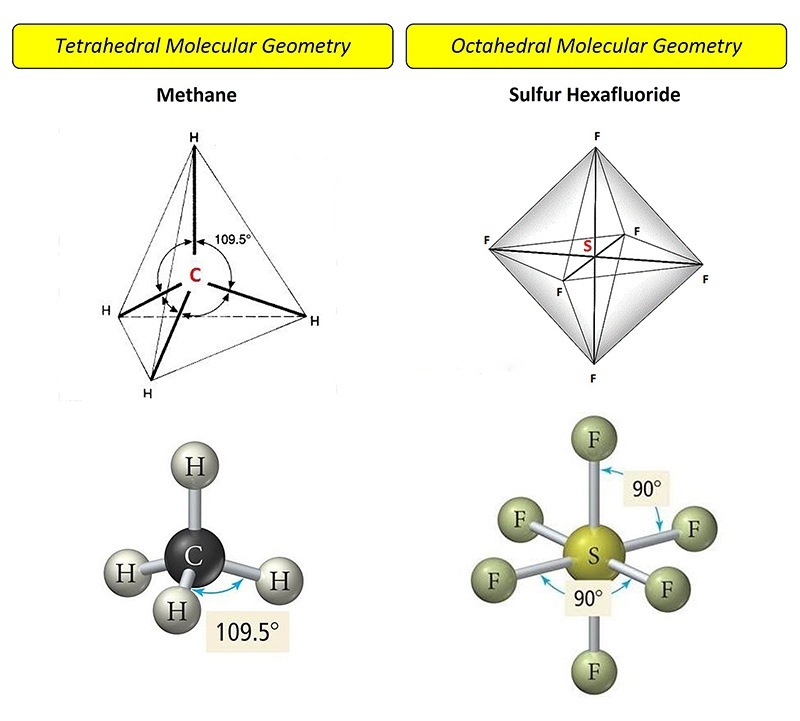
Three-dimensional molecular shapes (molecular geometry)

Molecular geometry is the three-dimensional arrangement of atoms within a molecule. Molecules are held together by pairs of electrons shared between atoms known as „bonding pairs“.

A molecule of methane (CH4) is structured with 4 hydrogen atoms (H) at the vertices of a regular tetrahedron bonded to one carbon (C) atom at the centroid. When the central atom has 4 bonding pairs, geometry is tetrahedral. All the angles between the two bonds are about 109,5°.

In a molecule of sulfur hexafluoride (SF6) six fluorine atoms (F) are symmetrically arranged around a central sulfur atom and joining together with 6 bonding pairs of electrons and defining the vertices of a regular octahedron. All the bond angles are 90°.

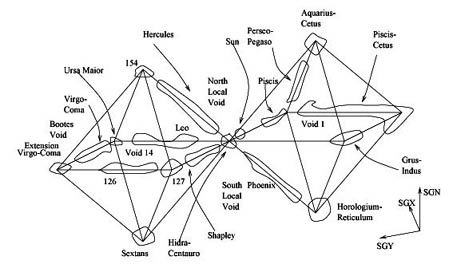
Clustering of the galaxies

Scientific observations made by astrophysics (E. Battaner and E. Florido) have shown that the Platonic solids can also be found in the clustering of galaxies. The distribution of super-clusters presents such a remarkable ordered pattern, like in these octahedron clustering of galaxies in the image below where the identification of real octahedra is so clear and well defined.

There are many more amazing examples showing the occurrence of the Platonic solids in nature.

Above the entrance of the famous Plato's Academy has been engraved a quote of which accurate translation there are still many disputes: "Let no one who cannot think geometrically enter."

On the contrary, I invite you to enter into the world of geometry and comment! Have you ever thought about geometry around us? Do you have favourite forms, shapes or patterns? Do you use geometry in your work?

Sources:

1. Minerals by Name

2. Wolfram MathWorld

3. https://towardsabetterworld.com

4. Alt.fractals: A Visual Guide to Fractal Geometry and Design

5. The Nature of Mathematics

6. The Royal Society

**********
 

If you like this buzz about geometry, please give it a "relevant" or a comment. If you really like it, please share.